математические модели
Модель оценки стоимости имущества
- 16 мая 2022, 12:07
- |
Придумал модель быстрой сравнительной оценки стоимости имущества с учётом накопленной за срок владения инфляции.
1. Смотрим модальную зарплату в этом городе в год покупки.
2. Делим сумму покупки имущества на модальную зарплату в тот год.
3. Получаем значение Х — это стоимость имущества, измеренная в модальных зарплатах этого города на день покупки.
4. Считаем модальную зарплату в год продажи имущества.
5. Умножаем её на количество модальных зарплат, уплаченных за данное имущество в год его покупки (тот самый Х).
6. Получаем справедливую сегодняшнюю цену объекта с поправкой на инфляцию.
Жду одобрения или критики предложенной модели.
- комментировать
- 363
- Комментарии ( 11 )
Лысина, математические модели и чтение отчетности
- 24 июля 2021, 07:50
- |
Подводная лодка фигачит на боевом дежурстве, советская атомная, здоровая, где-то там в Атлантике, набитая резиной, чтобы ее не хавали радары. Вот она плывет. И самая мрачная вахта всегда у капитана, «собачья» ее называют, – с 2 до 6 утра, когда все спят. И ему достается самый квалифицированный рулевой. Этот квалифицированный рулевой, некий мичман, полная ссс…., ну, очень нехороший. И ненавидит его этот капитан всей душой. Этот мичман не моется, во-первых, мотивируя тем, что он экономит пресную воду. Во-вторых, он омерзительно лысый, и голова у него квадратная. И, в-третьих, он все время спит. В любой ситуации. Изумительное зрелище. И вот мичман держит рули эти, а в учебке еще намертво вбивается навык – рули не бросать ни в коем случае. То есть, тебя могут убить, но рули бросать нельзя. И вот он держит эти рули и спит, падла. И так из вахты в вахту. И так это капитана злит! Это глупо, конечно. И о чем бы с ним он и говорил? Но вообще сама невозможность слово сказать! И думает: «Но вот почему так? И ко всему плохому еще и вот эта сучья рожа мичмана этого тупого с его лысиной, вонью!» И он думает: «Ну вот что ему сделать? Уколоть его в задницу? Ну, это детски как-то. Гаркнуть как-то? Опять заснет. Как его ущучить?» Об этом он думает неотступно.
( Читать дальше )
Можно ли делать прогноз цен математическими методами - на примере реальных торгов МБ
- 20 июля 2020, 20:52
- |
В продолжение дискуссий на сайте о том, что можно или нет прогнозировать цену, и о полезности математики в трейдинге.
Не судите строго — я никогда не работал диктором )))
Не Гарри не Марковиц
- 01 мая 2020, 20:12
- |
Как думаете, можно ли разработать методику формирования инвестиционного портфеля, которая показывала бы лучшие результаты, чем модель Марковица?
Или уже всё, большее совершенство недостижимо, и мы обречены?
Если да, то почему?
Если нет, то почему?
Шлако-портфель уходит в небо
- 12 апреля 2020, 22:11
- |
Пришла мысль проверить вот такую стратегию:
1. Находим все шлаки на Мосбирже (допустим, 500, хотя не знаю, сколько их здесь).
2. Покупаем в равных долях, на каждый выделяя минимальную сумму.
3. Пассивно ждём, пока весь портфель или отдельные его составляющие не увеличатся в цене в 20-50 раз.
4. После выстрела кроемся, высвободившийся капитал перераспределяем.
Пробовал ли кто-то похожее? Имеет ли смысл это проверять?
"Справедливые" цены на 9:00 10.10.19
- 10 октября 2019, 09:06
- |
Здравствуйте, дамы и господа!
В соответствии с математической моделью, описанной ранее, текущие цены отличаются от «справедливых» так:
Инструмент RMSE, % Отклонение, RMSE «Справедливая» цена Рекомендация
EURUSD 0.17 -0.013507192 1.098514 Нейтрально
USDJPY 0.21 -0.856945506 107.3087 Нейтрально
Золото 0.27 -0.46607180 1505.100 Нейтрально
Серебро 0.49 -1.073985291 17.73236 Продавать
S&P500 fut 0.39 0.3033849734 2919.028 Нейтрально
Brent 0.80 0.83885466 58.67105 Держать покупку
Мониторинг счета
( Читать дальше )
"Справедливые" цены на 9:00 03.10.19
- 03 октября 2019, 09:03
- |
Здравствуйте, дамы и господа!
В соответствии с математической моделью, описанной ранее, текущие цены отличаются от «справедливых» так:
Инструмент RMSE, % Отклонение, RMSE «Справедливая» цена Рекомендация
EURUSD 0.18 0.67703906 1.097007 Держать покупку
USDJPY 0.21 0.53907150 107.2364 Закрыть продажу
Золото 0.27 -0.12494432 1498.110 Закрыть покупку
Серебро 0.49 -0.90245396 17.48853 Закрыть покупку
S&P500 fut 0.39 0.24645088 2888.918 Нейтрально
Brent 0.79 1.48857766 58.22430 Держать покупку
Мониторинг счета
( Читать дальше )
Математическая модель рынка. Справедливые цены на 9:00 26.09.19
- 26 сентября 2019, 09:09
- |
Здравствуйте, дамы и господа!
В соответствии с математической моделью, описанной ранее, текущие цены отличаются от «справедливых» так:
Инструмент RMSE, % Отклонение, RMSE «Справедливая» цена Рекомендация
EURUSD 0.18 -0.03111250 1.088680 Нейтрально
USDJPY 0.21 -0.01023870 107.6616 Нейтрально
Золото 0.27 -1.04167173 1503.985 Продавать
Серебро 0.49 1.015527037 18.08502 Покупать
S&P500 fut 0.39 -0.24515529 2980.048 Нейтрально
Brent 0.78 1.33920603 61.99297 Покупать
Профита всем!
( Читать дальше )
Изучение простой модели котирования
- 21 декабря 2016, 13:16
- |
Как с помощью математики можно изучать рынок? Ниже приводится некий пример. При этом рынок, как известно, всегда прав, а модели только пытаются как-то ухватить его некоторые особенности. Не стоит идеализировать модели.
В нашей модели будем считать, что рынок суперликвидный, поэтому бид B и оффер O всегда отличаются на один шаг цены, который, для простоты, положим равным 1, т.е. O = B+1.
Цены в модели будут меняться дискретными тактами: с вероятностью p расти так, что пара бид-офер из (B, O) превратится на следующем такте в (B+1, O+1); с вероятностью q падать, давая новую пару бид-офер (B-1, O-1), и с вероятностью r = 1-p-q стоять на месте.
Допустим, мы хотим совершить покупку. Можно покупать по рынку (А), можно выставлять лимитную заявку в лучший бид и переставлять её, если рынок уходит выше (Б), можно отступать от лучшего бида вниз на один шаг цены, выставлять лимитную заявку там и переставлять её, если цена поменялась, а заявка ещё не исполнилась (В). Посмотрим, какая цена исполнения получится для каждого из этих трёх способов.
( Читать дальше )
Модель скрытых состояний Маркова. Часть 2
- 14 мая 2015, 13:34
- |
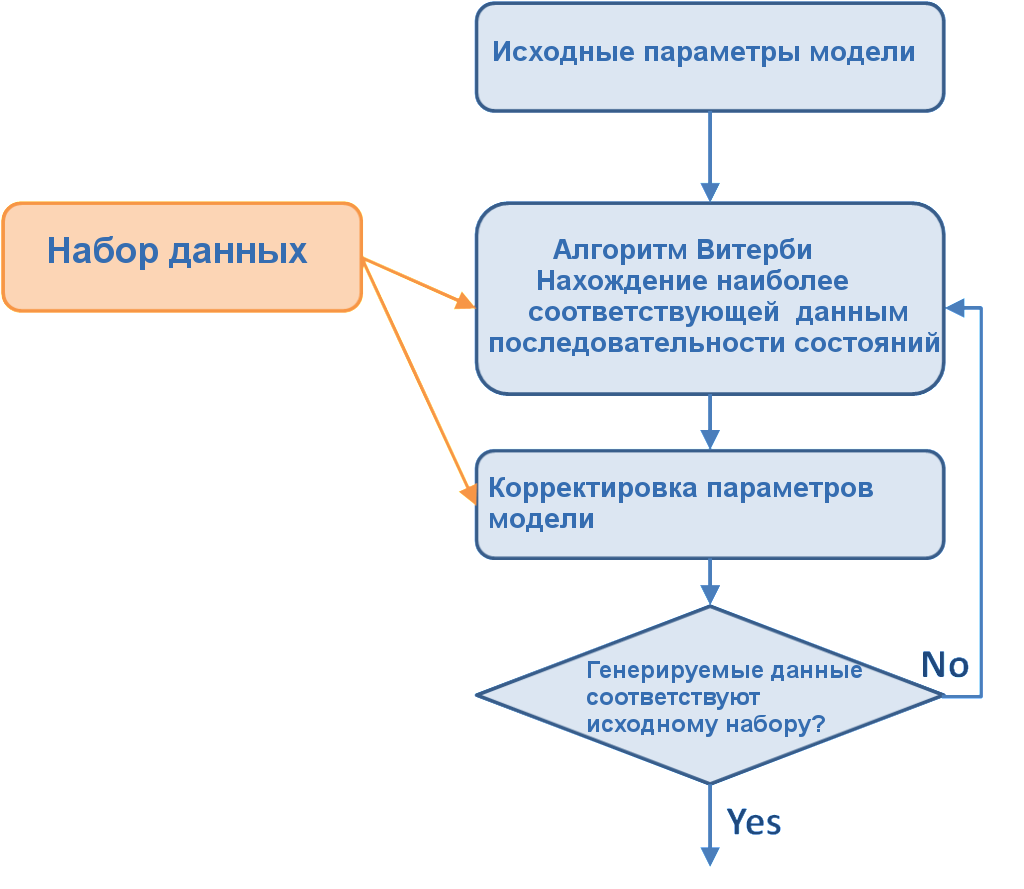
В предыдущей статье мы говорили об эффективных алгоритмах, необходимых для вычисления вероятностей и стат. распределений модели Маркова, которыми являются форвардный алгоритм и алгоритм Витерби. Форвардный алгоритм вычисляет вероятность соответствия данных наблюдения полученным моделью всем возможным последовательностям состояний. Алгоритм Витерби вычисляет вероятность соответствия данных полученной моделью одной, наиболее вероятной, последовательности.
В этом посте будет много формул, но без этого не обойтись, чтобы создать хорошую стратегию, надо разбираться в математической модели, лежащей в ее основе. Следующие части будут более приближенными к практике.
Форвардный алгоритм.
Форвардный алгоритм позволяет эффективно рассчитать функцию вероятности p(O|λ). Форвардной переменной называется вероятность генерации моделью наблюдений до времени t, и состояние j в момент времени t определяется как:
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nyse
- rts
- s&p500
- si
- usdrub
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновая разметка
- волновой анализ
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- дональд трамп
- евро
- золото
- инвестиции
- инвестиции в недвижимость
- индекс мб
- инфляция
- китай
- ключевая ставка цб рф
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал